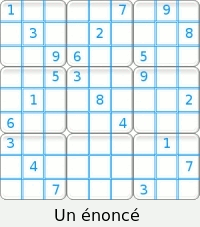
Techniques et aide de résolution de sudoku

Une grille sudoku complète est un tableau de 9 cases sur 9, subdivisé en 9 carrés de 3 cases de côté. Chaque case contient un seul chiffre allant de 1 à 9. Chaque ligne, colonne, et carré de 3 X 3 incluent obligatoirement ces 9 chiffres. Par conséquent, pris isolément, une ligne, une colonne ou un carré de 3 sur 3 ne peuvent contenir plusieurs fois une même valeur.
Un énoncé sudoku est une grille incomplète n'acceptant qu'une solution unique.
Nous appellerons indifféremment grille, un énoncé en cours de résolution ou la solution complète de celui-ci.

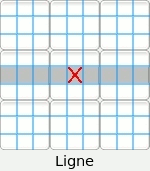
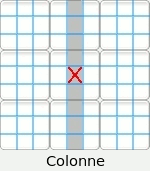
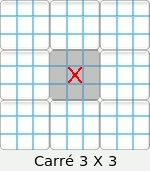
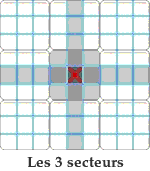
Nous appellerons « secteur d'une case » la ligne, la colonne ou la région carrée de 3 X 3 dans lesquels une case est incluse. Par exemple la case centrale appartient aux trois secteurs suivants :

En résumé les trois secteurs d'une case sont soumis à la même contrainte :
Ils contiennent chacun les chiffres allant de 1 à 9 sans possibilité de répétition.

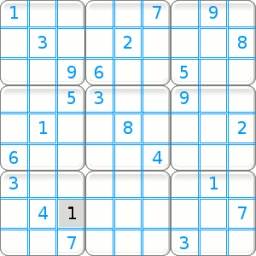
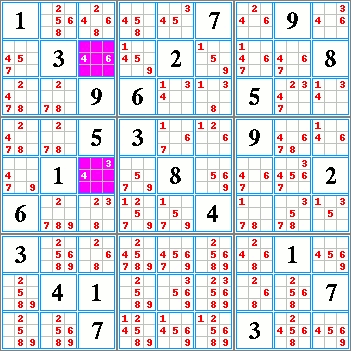
Attention : Le terme « région » définit un carré de 3 X 3. Le terme « secteur » indique indifféremment la ligne, la colonne ou la région carrée afférente à une case.

Méthodes de résolution.

Nous ne développerons uniquement ci-dessous que les procédures utilisées par le résolveur du site. Nous rajouterons ultérieurement d'autres méthodes au fur et à mesure des améliorations du logiciel.

Il y deux types principaux de méthode.
• Celles solubles directement par un schéma visuel ou par la lecture des candidats.
• Celles solubles exclusivement par la lecture des candidats.

On appelle candidats d'une case les chiffres possibles que cette case peut admettre. L'ensemble des candidats d'un énoncé sudoku sont toutes les possibilités de toutes les cellules de la grille. Le site vous permet de les afficher à tout moment.

Il est conseillé, pour faciliter la tâche, de commencer à résoudre visuellement le maximum de cases pour terminer avec le minimum de candidats à écrire.

Les quatres méthodes de base :

Conduite par inclusion.
  • Visuellement ou par lecture des candidats.
Conduite par exclusion.
  • Visuellement ou par lecture des candidats.
Conduite par paires exclusives.
  • Par lecture des candidats.
Choix multiples.
  • Par lecture des candidats.

Conduite par inclusion.

Une case admet un chiffre si l'ensemble des trois secteurs de cette case ont déjà inclus les huit autres chiffres.
Cette méthode est soluble visuellement ou par l'étude des candidats marqués.

Approche visuelle :
Exemple : Les trois secteurs de la case violette L4C9, ont déjà inclus huit valeurs, en vert : 7, 2, 3, 4, 6, 1, 5 et 9. Il ne reste par conséquent que le 8 comme solution.

Méthode inclusive visuelle d'une grille sudoku.

Il n'y a pas de système optique particulier à appliquer. Le regard doit s'attarder sur les cases en rapport avec le plus grand nombre de chiffres possibles. Par exemple la case grise L3C4 n'est guère intéressante, car elle n'est en relation qu'avec deux nombres.

Dans cette grille une deuxième case admet une solution par inclusion. La trouverez vous ?

Lecture des candidats marqués :
Une case n'ayant qu'une possibilité a forcément cette possibilité comme solution. La case violette L4C9 ne possède bien qu'un seul candidat et confirme l'aproche visuelle ci-dessus.

Méthode inclusive détaillée d'une grille sudoku.

Avez-vous trouvez la deuxième case ?!

Pour vous entraîner à cette technique, toutes les grilles de niveau débutant de ce site sont solubles intégralement par inclusion.

Conduite par exclusion

Une case admet un chiffre si celui-ci est exclu de toutes les autres cases d'un des secteurs afférents à cette case.
On remarquera qu'une case acceptant une solution par exclusion a normalement plusieurs candidats possibles. Sinon cette case est décidée plus simplement par inclusion.

Cette méthode est soluble visuellement ou par l'étude des candidats marqués.

Trois types de cas sont possibles :
  • Conduite par exclusion dans un carré 3 X 3.
  • Conduite par exclusion dans une ligne.
  • Conduite par exclusion dans une colonne.

Pour vous entraîner à cette technique, toutes les énoncés de niveau confirmé de ce site peuvent être complétés intégralement par inclusion et exclusion.

Conduite par exclusion dans un carré 3 X 3

Grille Confirmée n° 7218 :

L'exemple, du schéma visuel à droite, indique comment le chiffre 2 est exclu des cases du secteur formé par le carré orange, excepté la cellule violette L4C2.
Par conséquence la case violette est la seule cellule de cette région à accepter le 2. Donc celui-ci est la solution de cette case.
L'oeil doit s'exercer à projeter les chiffres sous la forme de droite.

Méthode exclusive visuelle d'une région de grille sudoku.

Méthode exclusive détaillée d'une région de grille sudoku.

Grille Confirmée n° 7218 :

A gauche, la lecture des candidats marqués du carré grisé, confirme que le chiffre 2 n'est uniquement présent, dans cette région, que sur la case violette L4C2.

Dans cet énoncé, une deuxième case accepte une solution par exclusion. La trouverez vous ? Solution ci-dessous.

Conduite par exclusion dans une colonne

Méthode exclusive visuelle d'une colonne de grille sudoku.

Grille Confirmée n° 7218 :

Dans l'exemple de gauche, tous les 9 sont expulsés des cases de la colonne 2, sauf dans la cellule violette en L7C2.
Le regard doit aussi s'habituer à couvrir des carrés de 3 X 3.

Grille Confirmée n° 7218 :

Sur la droite, la lecture des candidats marqués de la colonne grisée, témoigne que le chiffre 9 n'est présent, dans ce secteur, qu'à l'intérieur la case violette L7C2.

Méthode exclusive détaillée d'une colonne de grille sudoku.

Conduite par exclusion dans une ligne

Méthode exclusive visuelle d'une ligne de grille sudoku.

Grille Expert n° 10.000 :

Dans l'exemple de gauche, tous les 9 sont rejetés des cases de la ligne 2, exceptée la cellule violette L2C7.
Ici le regard doit circonscrire cinq zones :
Les deux premiers carrés de 3 X 3, les deux colonnes de droite, ainsi que la ligne 2.

Grille Expert n° 10.000 :

Sur la droite, la lecture des candidats marqués de la ligne grisée, corrobore le schéma précédent : Le chiffre 9 n'est présent, dans ce secteur, que dans la case violette L2C7.
On remarquera que la cellule L2C7 est soluble malgré six postulants possibles...

Méthode exclusive détaillée d'une ligne de grille sudoku.

Conduite par paires exclusives

Cette méthode nécessite l'observation de l'ensemble des candidats marqués de la grille et implique deux conjectures
1ère condition : Si dans un secteur deux cases contiennent la même paire de chiffres alors ces chiffres peuvent être exclus des autres cases de ce secteur.
2 ème condition : Si suite à cette exclusion une case se retrouve avec un seul candidat possible alors ce candidat est la solution de la case.

Deux types de cas se présentent :
• Exclusion d'un chiffre.
• Exclusion de deux chiffres.

Paire exclusive à un chiffe

Méthode paire exclusive à 1 chiffre d'une grille sudoku.

Le sudoku expert n° 2616 en cours de résolution :

Observons la colonne 4.

Les deux case vertes, L3C4 et L9C4, contiennent les candidats 3 et 7. Ce sont les deux seules cases de cet secteur à posséder cette paire de possibilités. Donc le 3 et le 7 sont forcément les solutions de ces deux cases.
Donc la case violette L1C4 exclut le 7. Par conséquent le 6 se retrouve être le postulant unique de cette case.
Donc le 6 est la solution de L1C4.

Paire exclusive à deux chiffes

Méthode paire exclusive à 2 chiffres d'une grille sudoku.

La grille expert n° 8131 en cours de résolution :

Analysons la ligne 5.

Les deux case vertes, L5C1 et L5C2, contiennent les postulants 4 et 8. Ce sont les deux seules cellules de ce secteur à posséder cette paire de candidats. Donc le 4 et le 8 sont obligatoirement les réponses de ces deux cases.
Donc le 4 et le 8 sont expulsés de la case violette L5C7. Par conséquent le 7 se retrouve être la possibilité unique de cette case.
Donc le 7 est la solution de L5C7.

Choix multiples

La technique des choix multiples n'est pas à proprement parler une méthode de résolution à part entière mais plutôt une roue de secours en cas de dernière extrémité.
Si aucune case ne trouve de solution on choisit alors une des cellules ayant le moins de possibilités. On essaie au hasard un des postulants de cette case et on tente de résoudre le reste de la grille. Si on aboutit à un cul-de-sac on retourne en arrière à la case de départ des choix multiples et on repart avec un autre candidat.

Aperçu visuel d'un choix multiple d'une grille sudoku.

L'exemple ci-contre à gauche est un énoncé appelé « Al Escargot ». C'est à ce jour la grille sudoku connue la plus difficile à résoudre.

Les chiffres de l'énoncé sont en bleu. La case grisée L8C3 est la première cellule acceptant une solution, le chiffre 1, par exclusion.

A partir de cette situation observons ci-dessous le tableau des candidats.

Il semble qu'il n'y ait pas de méthode pour résoudre une des cases de ce problème.
Il s'avère dans ce cas qu'il faille prendre au hasard un des postulants d'une des cellules possédant le moins de candidats possibles. Ici le 4 ou le 6 en L2C3 sinon le 3 ou le 4 en L5C3.
Si quelqu'un trouvait une méthode de résolution pour une des cases ici présentes, qu'il nous écrive. Nous citerons avec plaisir cette performance sur le site.

Méthode détaillée par choix multiple d'une grille sudoku.

Méthodes de résolution non encore exploitées par le site

Les n-exclusives. C'est à dire tout comme les paires exclusives, les triplets, quadruplets exclusifs etc...

Les solutions croisées ou solutions dites de niveau n.
Une paire ou une n-exclusive peuvent supprimer des postulants dans une case "x" sans pour autant résoudre celle-ci. Mais cela peut aboutir à la résolubilité d'une autre cellule "y" en rapport avec la case "x" précédemment simplifiée...

En savoir plus. En poursuivant votre navigation, vous acceptez l'utilisation de cookies pour réaliser des statistiques de visite, vous permettre de partager les contenus sur les réseaux sociaux et personnaliser les encarts publicitaires.

Recommendez sur
sur Google

W3C/HTML5 W3C/CSS