Suite à la réglementation européenne sur la protéction de données (RGPD), nous vous informons que nous utilisons des cookies pour vous garantir la meilleure expérience sur ce site Web, pour personnaliser les publicités (qui permettent la gratuité de ce site) et pour analyser le trafic du site.
Si ce message apparait sans arrêt à toutes ouvertures de pages cliquez sur "En savoir plus".En continuant à naviguer sur notre site, vous acceptez l'utilisation de ces cookies qui permettent de compiler des statistiques de visites et personnaliser les inserts publicitaires.
Aide et technique de résolution
Grilles sudoku de 9 x 9
Méthode par choix multiple
La technique des choix multiples n'est pas à proprement parler une méthode de résolution à part entière mais plutôt une roue de secours en cas de dernière extrémité.
Si aucune case ne trouve de solution on choisit alors une des cellules ayant le moins de possibilités. On essaie au hasard un des candidats de cette case et on tente de résoudre le reste de la grille. Si on aboutit à un cul-de-sac on retourne en arrière à la case de départ des choix multiples et on repart avec un autre candidat.
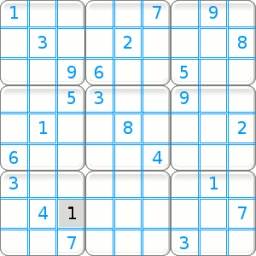 | L'exemple ci-contre à gauche est un énoncé appelé « Al Escargot ». C'est à ce jour la grille sudoku connue la plus difficile à résoudre.
Les chiffres de l'énoncé sont en bleu. La case grisée L8C3 est la première cellule acceptant une solution, le chiffre 1, par exclusion.
A partir de cette situation observons ci-dessous le tableau des candidats. |
Il semble qu'il n'y ait pas de méthode pour résoudre une des cases de ce problème.
Il s'avère dans ce cas qu'il faille prendre au hasard une des possibilités d'une des cellules possédant le moins de candidats possibles. Ici le 4 ou le 6 en L2C3 sinon le 3 ou le 4 en L5C3.
Si quelqu'un trouvait une méthode de résolution pour une des cases ici présentes, qu'il nous écrive. Nous citerons avec plaisir cette performance sur le site. | 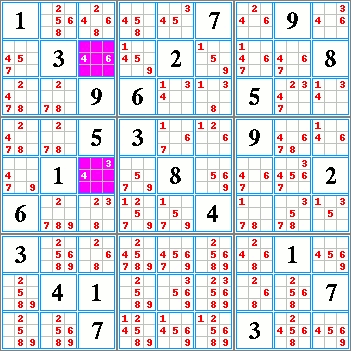 |

